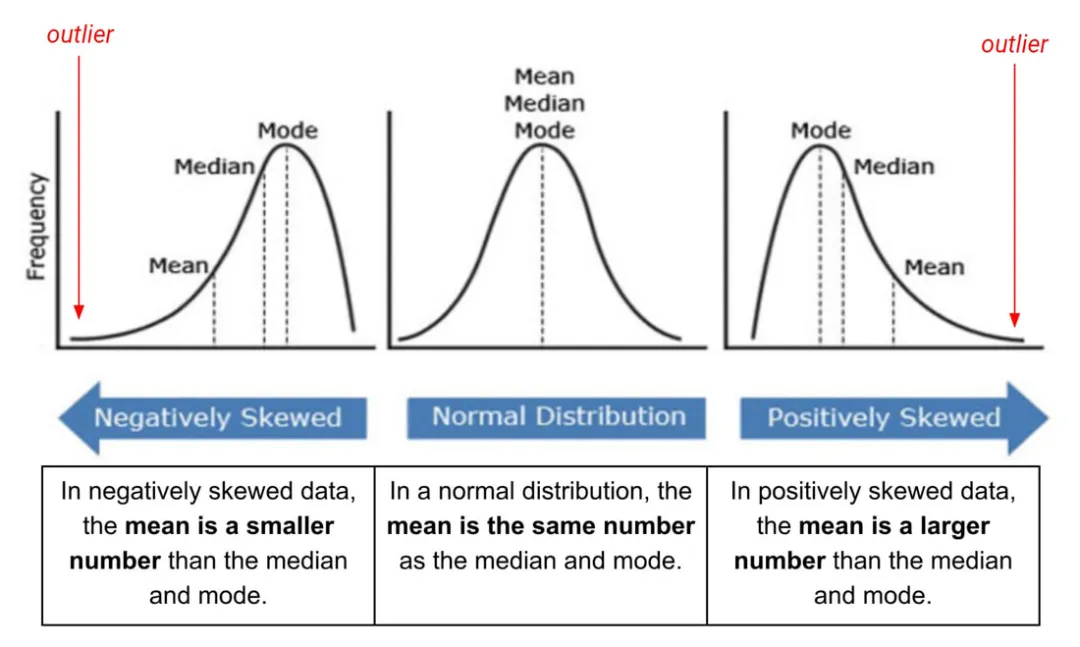
数据清洗 - 处理异常值中，DMSAS的惊人表现！

数据科学中的重要一步是清理数据。

这包括识别和删除可能由于数据收集错误或其他因素导致的数据点，以避免对数据得出错误的结论。

这与“操纵”数据,为了得到想要的结果而修改数据不同, 为了得到想要的结果而修改数据属于造假，而针对异常值的处理是排除由于各种原因导致的数据错误，以获取到更为客观、接近事实的结果。

数据清洗涉及一系列专门设计的方法，用于识别和去除客观异常的数据点。也就是说，有客观理由去除它们。

在编写研究报告时，数据清洗的步骤应始终被记录，以确保分析的透明性和可重复性。

太长不看版：

01异常值的识别与处理方法

定义：异常值是显著不同于大多数数据点的数据点，可以通过不同标准判断。

判断方法

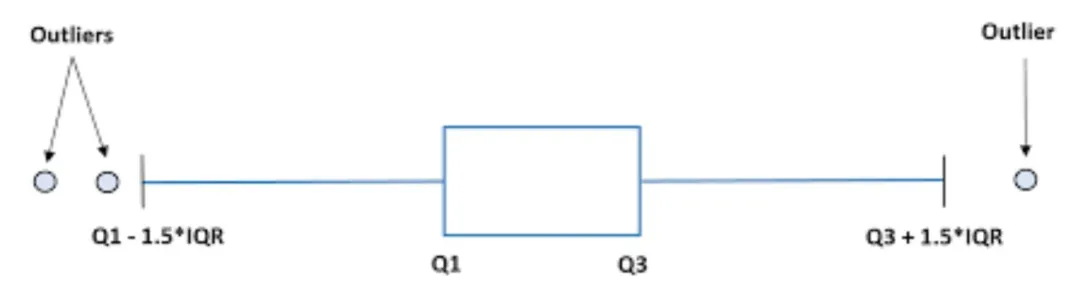
Tukey方法：基于四分位距（IQR），1.5倍IQR范围外的点即为异常值。

标准分数（z转换）：数据点转化为标准分数，z > 3 或 z < -3 的数据点为异常值。

异常值的处理方式

1. 忽略异常值： 通常不建议忽略，除非有明确的理由认为异常值有意义或数据不是正态分布。
2. 从数据集中移除： 对于重复测量数据可移除个别异常值，但单次测量时需谨慎，避免数据丢失影响分析。
3. 用非异常值替代： 可用均值或最极端的非异常值替代异常值，甚至还可用knn、线性预测等算法推测出一个值来代替异常值，这样可以减小异常值对统计结果的影响。

啰嗦版：异常值的识别与去除

异常值的定义：

异常值是指与数据集中大多数数据点“显著不同”的数据点。

“显著不同”在此打引号，因为它并不一定意味着我们使用统计检验来定义异常值，并且关于“显著”的定义也有多种方法。换句话来讲，关于异常值判断根据不同方法有不同的标准。

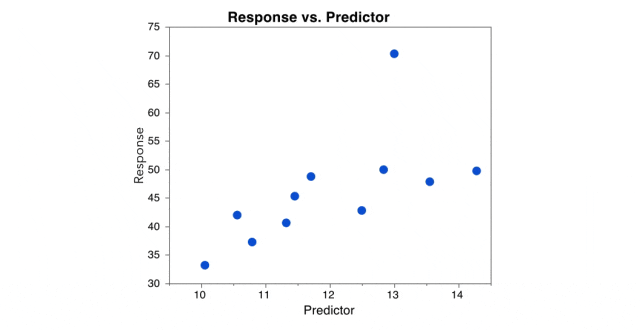
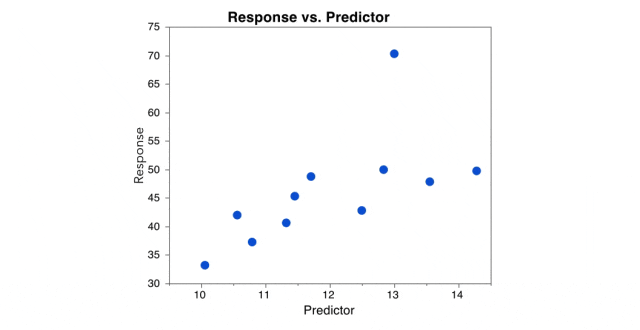
判断异常值的方法：Tukey方法

约翰·图基在发展探索性数据分析时，定义异常值为超出某个范围的数据点。四分位距（IQR）是数据集中涵盖50%数据点的范围。

在箱形图中（由图基发明），IQR是“箱体”，而1.5 IQR是从中位数向每个方向延伸的“须”的长度。在箱形图中，异常值表示为超过“须”的单个点。

一般来说，如果数据大致呈正态分布，用这种方法定义的异常值约占1%。

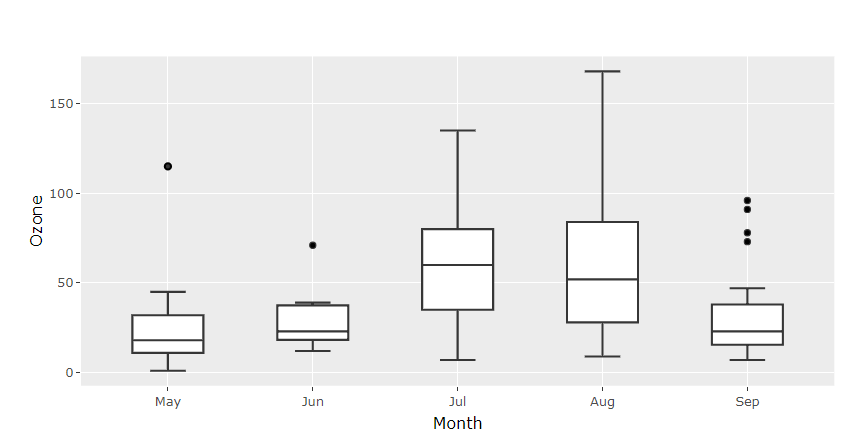
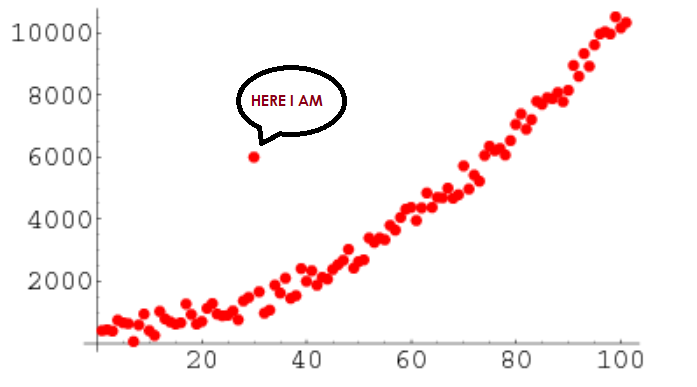
图上黑色的实心黑点就是异常值

标准分数

另一种方法是使用标准分数，即对数据应用z转换。

其公式为：

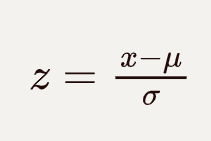
其中，x为单个数据点，μ为数据集的均值，σ为标准差。z转换将数据集转换为均值为0、标准差为1的标准单位。

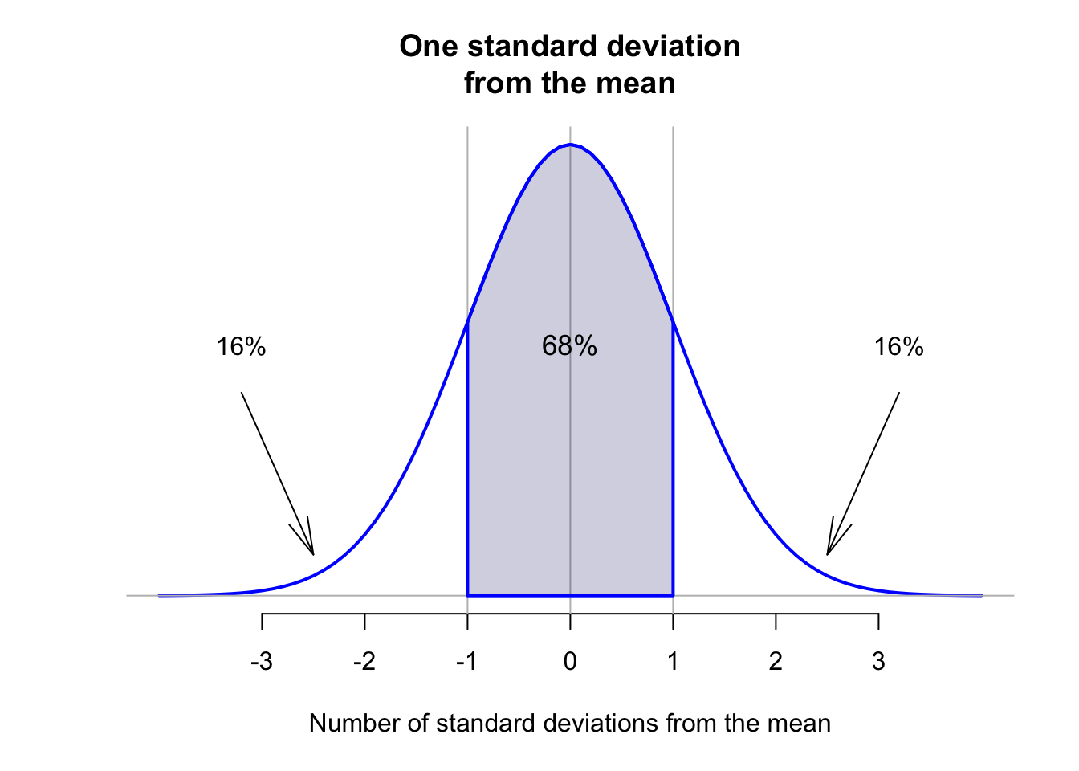
在正态分布中：

1. 68.27%的值位于均值的±1个标准差以内，
2. 95.45%的值位于±2个标准差以内，
3. 99.73%的值位于±3个标准差以内。

因此，如果我们定义异常值为那些z>3或z<−3的值，我们将排除大约0.25%的数据集。有时也会使用z±2.5作为标准，这样会排除更多的数据点（通常约2%）。

为什么异常值是个问题？

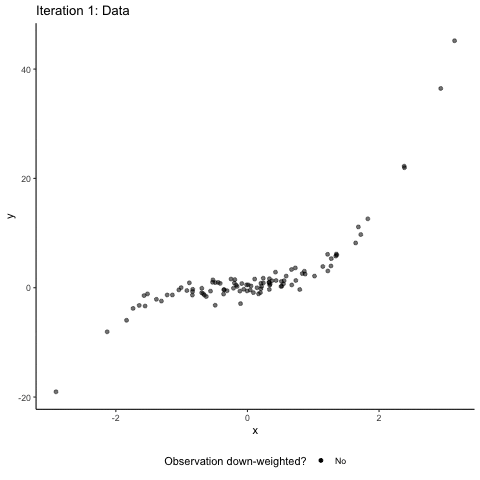
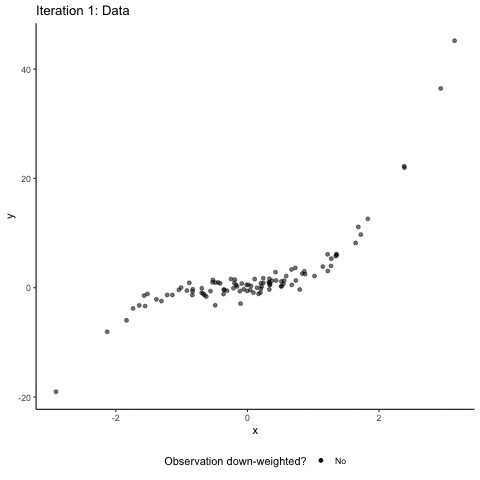
异常值会对统计属性如均值和方差产生不成比例的影响。

通过模拟数据可以看到，异常值越大，对均值和方差的影响越大。

异常值的影响取决于数据集的大小和异常值相对于其他数据值的大小。

如何处理异常值

对于异常值，我们有三种基本选项：

1. 忽略它们——直接将其包含在数据和所有分析中。
2. 从数据集中完全移除。
3. 用非异常值替代。

一般建议是不要忽略异常值，除非有充分、明确的理由说明为什么异常值可能有意义或不是真正的异常值。

1.忽略异常值

一些研究者根本不认为应排除异常值。

在处理人类或动物参与者的数据时，可以认为任何行为反应都有可能是有效的，异常值可能代表了有趣的数据点，原因可能多种多样（例如，反应时间（RT）特别慢可能意味着个体花了很多时间思考刺激并试图决定如何反应）。

另一个不移除异常值（或使用其他定义方式）的原因是，如果数据实际上不是正态分布。

事实上，我们正在处理的反应时间数据并非正态分布，而是偏态分布——这是一个相对较小的正态性违背。

尽管正态分布在自然界中很常见，但并非所有数据都是正态分布的，因此检查数据的分布情况是有价值的（这也是我们花很多时间查看箱形图、直方图和其他分布可视化的原因之一）。

另一方面，异常值可能是由实验之外的原因产生。

例如，异常值是客观真实存在的。

建议除非有强有力且合理的理由认为异常值可能是有趣的（或数据分布不是正态的，因此它们不是真正的异常值），以及对这些异常值的解释方法，否则不要忽略异常值。

2.从数据集中移除

移除数据点（即修剪或截断）在某些情况下是可以接受的，但在其他情况下则存在问题。

对于重复测量数据，通常可以在个别参与者层面移除异常值，因为我们有很多其他测量样本（如重复测量中的试验）。

另一方面，如果我们对实验设计中的某一“单位”（如每个参与者在每个条件下仅有一次测量）仅有一次测量，则可能不希望完全丢失该数据点。这在使用t检验或ANOVA进行统计分析时尤其重要，因为这些方法无法处理缺失值。

3.用非异常值替代

另一种处理异常值的方法是用较不偏离的值替代它们。

这可以是均值，或不被视为异常值的最极端值。

用均值替代异常值基本上是“中和”了该数据点，因为它相当于均值，不会改变数据点的均值。然而，这会人为地略微降低数据的方差，因为方差的定义是数据点偏离均值的量。

如果只替换1-2%的数据值，那么对方差的影响应该相对较小。此外，正确地说，用作替换值的均值应仅从所有非异常数据值中计算得出。这是因为最初替换或移除异常值的一个主要原因是它们对均值的影响过大。

将异常值替换为最极端的非异常值将保留该数据点对方差的贡献，但相较于保留异常值会减少方差。

同样，对均值的影响不会完全中和，但也会相对较小。

需要注意的是，用另一个相对极端的值（相对于均值）替换异常值的假设是，异常值实际上是一个有效测量，只是可能带有一些噪声。

由于我们不能确定数据的真实值，因此原则上用均值替换异常值是更好的选择。

02DMSAS中针对异常值的处理

示例数据

模拟生成了一段包含三个异常值的数据，如下：

1  Value    

2  Min.    : 26.91  

3  1st Qu.  : 45.06  

4  Median  : 51.17  

5  Mean   : 55.46  

6  3rd Qu. : 58.26  

7  Max.   :250.00

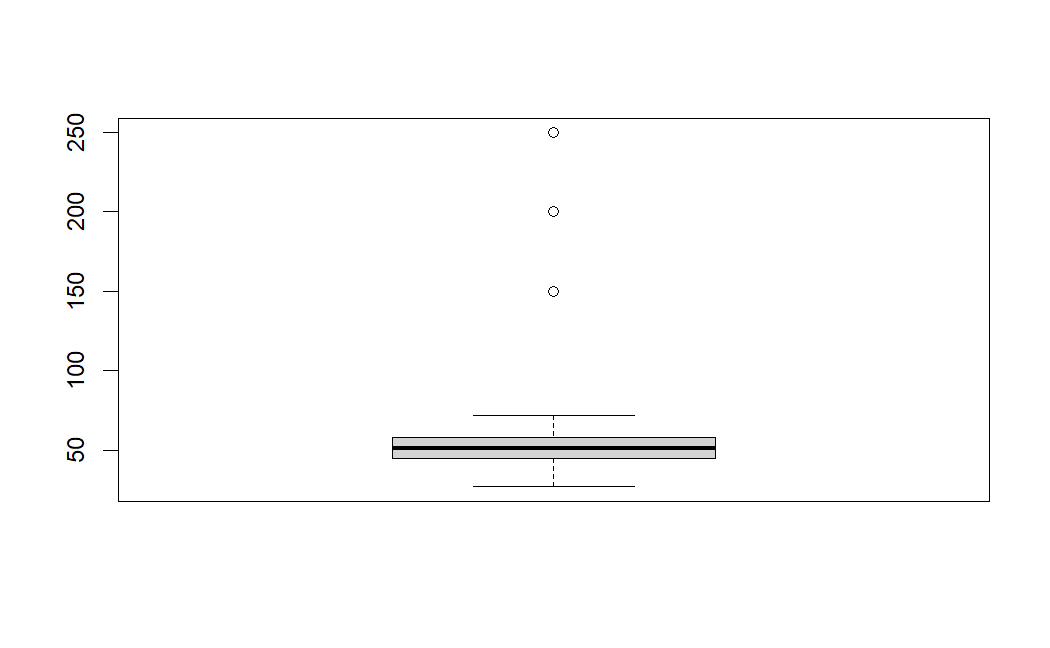从箱线图可以看到三个明显异常分布的散点，如上描述的，箱线图根据1.5 IQR为判断标准定义异常值。

在DMSAS中处理异常值

1.异常值的判定

在DMSAS中处理异常值不可谓不简单，简单到其实没啥好讲的，如下图所示，导入数据后，点击界面中的异常值处理即可。

在跳出的异常处理界面中，可选择异常值判断标准，DMSAS内置了两种判断标准，一种是根据数据偏离均值多少倍标准差，另一种就是偏离的百分比，其实本质就是我们在上述中介绍的两种方法。

此外，DMSAS还提供了一个自定义选项可供我们用其他方法鉴定异常值，不可谓不贴心。

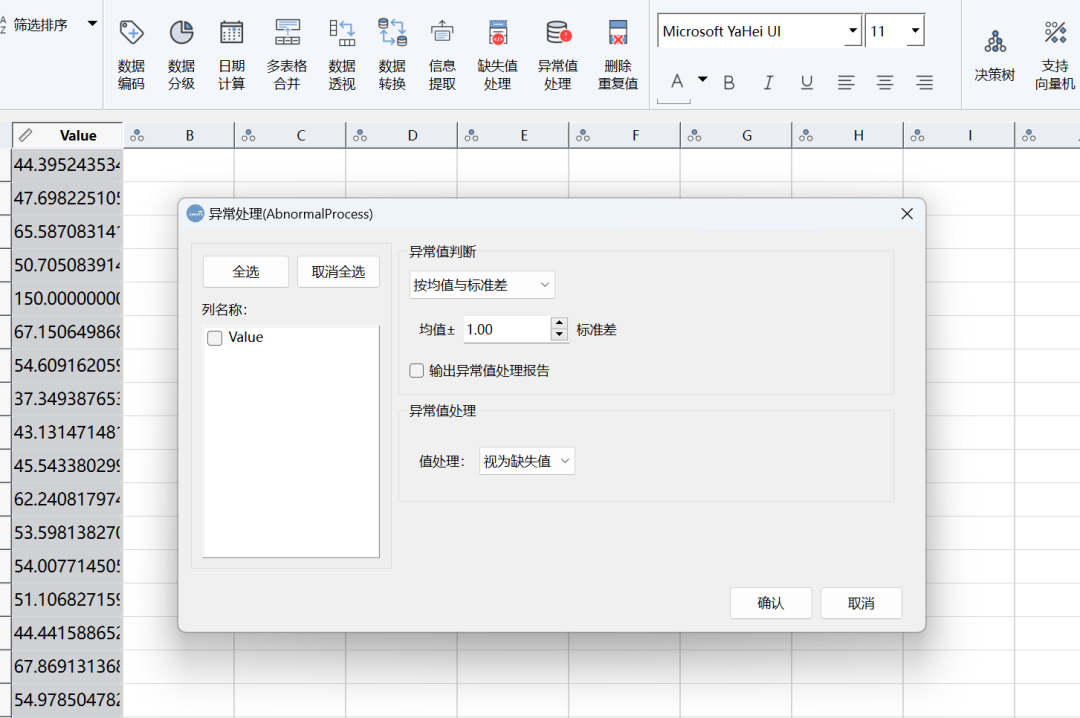
2.异常值的处理

在DMSAS中对异常值的处理也是极为简单的，处理方式如前面介绍的，有直接删除（视为缺失值）和非异常值替代。

在DMSAS中，利用非异常值替代异常值，除了均值替代外，还有其它多种方法，甚至包括利用knn和线性算法等机器学习方法推测值来替代异常值。

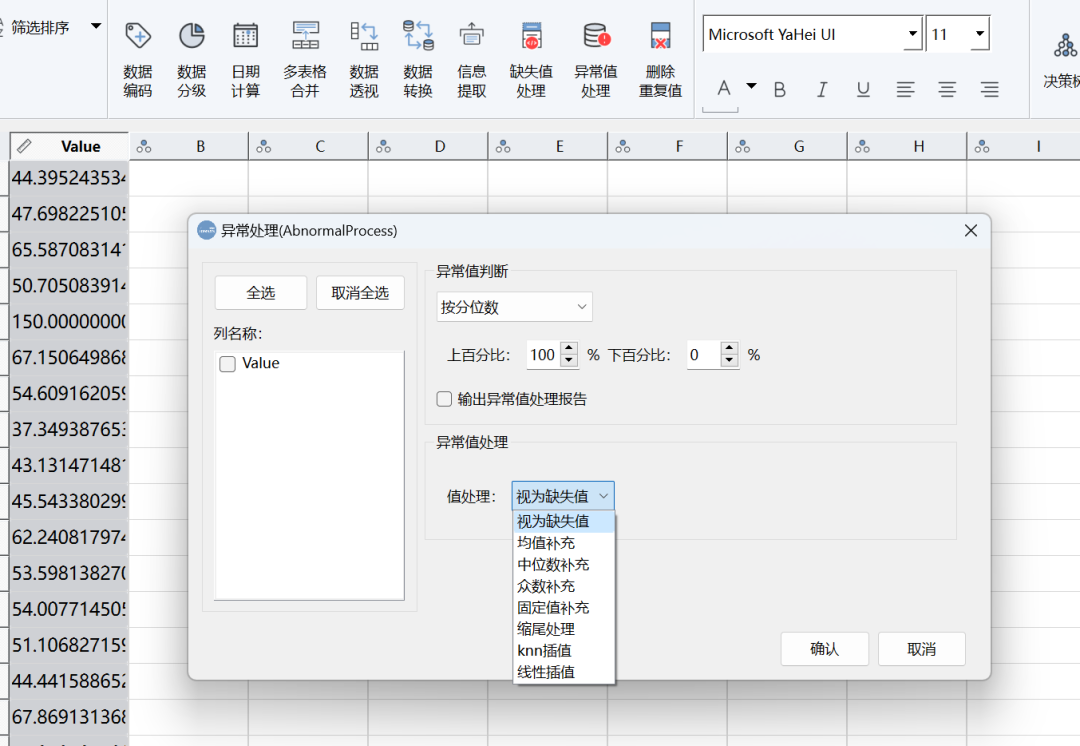
此外 ，这里还有一个值得推荐的方法，就是在异常值处理这一步呢，先将异常值直接删除，即视为缺失值。然后在具体建模分析的时候，再利用其他方法处理缺失值。

这样有个好处就是不必重复进行异常值处理，可以在建模的那一步根据模型结果进行选择合适的异常值处理方式。

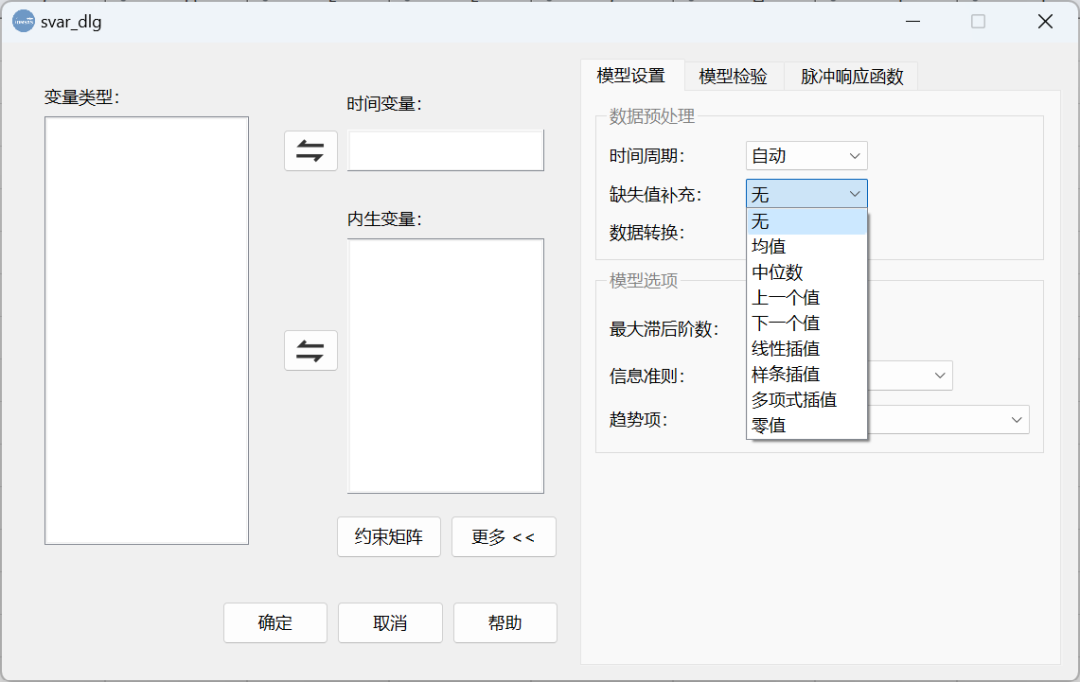
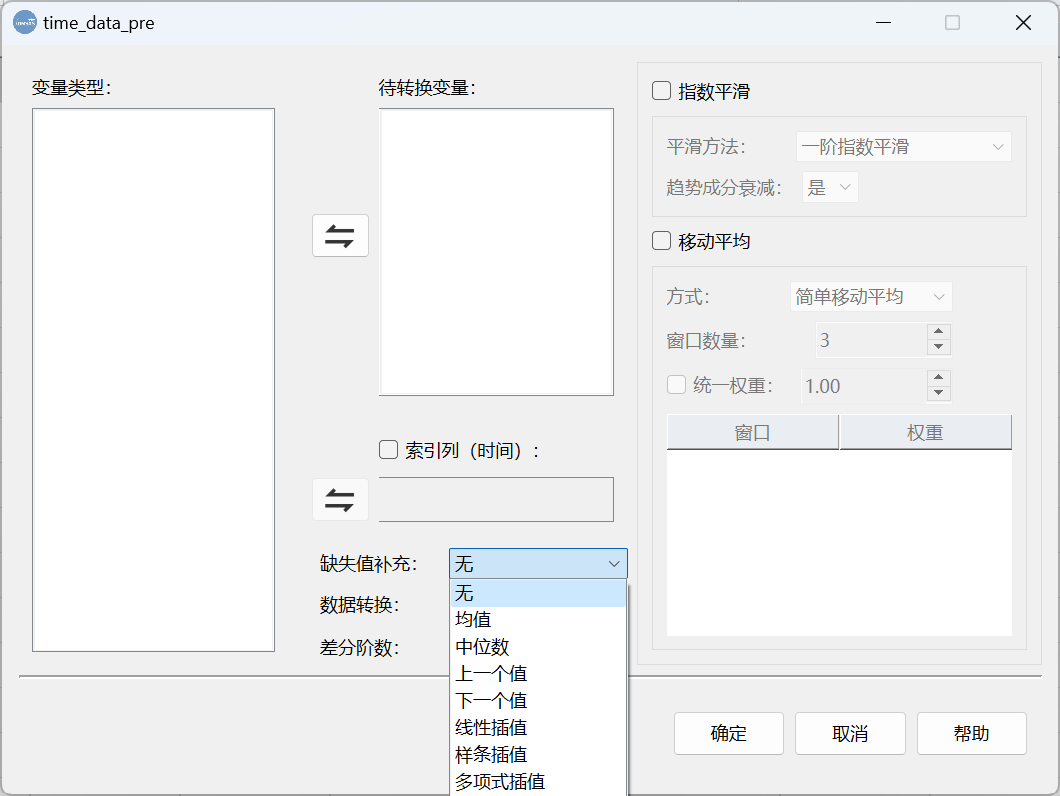
这是因为在DMSAS中的许多建模分析过程都有一个缺失值处理选项，例如时间序列的处理中就可以选择线性插值、样条插值、多项式插值等等方式填补缺失值。

这就是使用DMSAS的便捷之处，让我们能够专注于研究的问题本身，而非在数据的各种“小问题”上（小问题：貌似很简单，但是被忽略的话会极大干扰数据结果）。