通俗易懂的详解t分布与t检验

t检验是我们刚涉及统计学知识就会接触到的一种检验方法，它繁琐的检验步骤总会让入门统计学的同学感觉很困扰：什么情况下要做t检验？单样本t检验，配对样本t检验，独立样本t检验使用的场景是什么？做t检验之前为什么要做正态检验？方差齐性检验？

这篇文章尽量避免套用大量的数学公式，全局梳理一下t分布和t检验的相关知识。

（本文章若有错误或纰漏之处欢迎朋友们在评论区积极指正。）

一切的根源在于无法获取全量样本

例如当前很火热的一个话题：华为Mate 60 pro更受欢迎还是iPhone 15 pro更好？

假如小明同学的研究课题就是如此，那么他可能会设计一个问卷试验，请不同的使用者为这两款手机打分，最终比较双方阵营的平均分。我们假设他的调研场景如下：小明在一个商场内随机向受访者发放问卷请他们给两款手机打分，共收集到关于iPhone 15 pro和Mate 60 pro相关问卷各60份，其中Mate 60 pro平均得分9.7，iPhone 15 pro平均得分9.5（满分都为10分）。于是得到研究结论：Mate 60 pro比iPhone 15 pro更受欢迎。

问题来了：国内使用苹果或华为手机的客户可能有上千万人，120位顾客的打分就把这两款手机分出了高下？这个结果可信么？

其实上述问题的解决方法倒是显而易见：我们将全国使用手机的人全部集中起来，请他们填写问卷为两款手机打分，这样得到的调查结果就有足够的力度了，然而这一做法完全行不通。小明内心其实也是有苦说不出：“你们在质疑我的结果，可我也是花了很大的精力才收集到的120份问卷啊，我真的收集不到更多了！”

理想很丰满，现实很骨干，这是科研中常有的事情。既然给全国人民发问卷的方式行不通，那我们只能想办法证明一下，这120份问卷的调研结果还是可以通过抽样来反映一些总体的问题的。至此，t分布与t检验就要登场了！

1 t分布

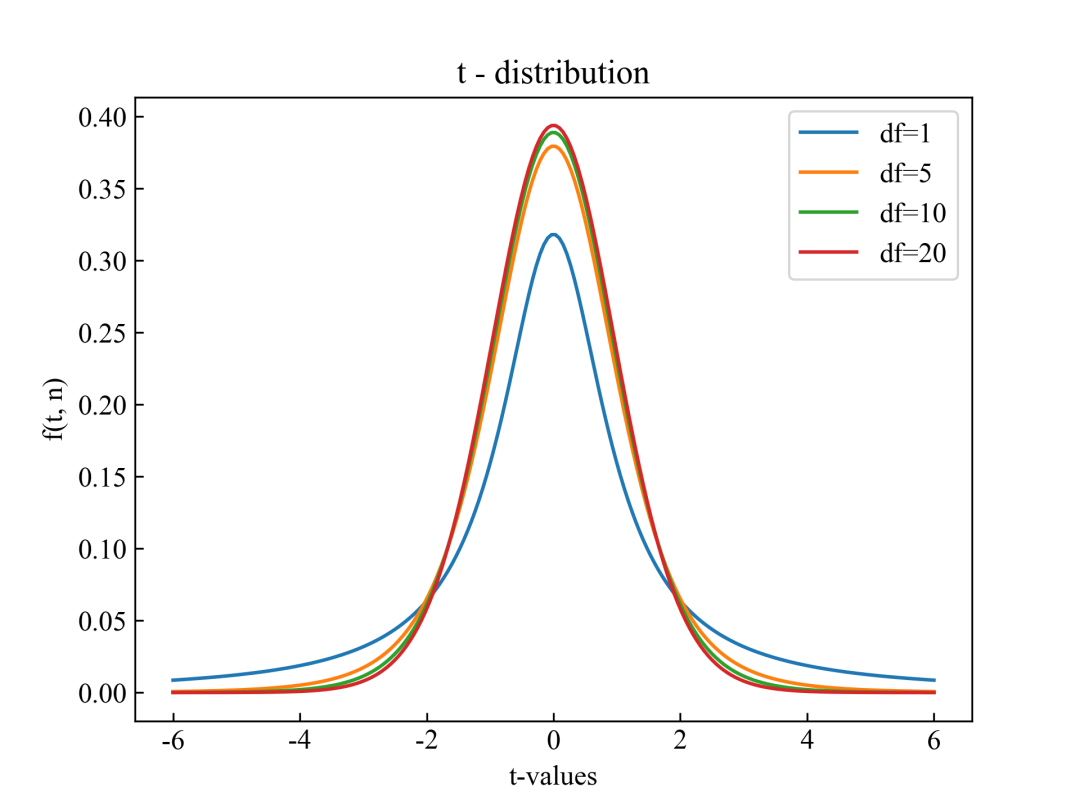首先让我们引入t分布的定义：当一个随机变量X服从标准正态分布，而另一个随机变量Y服从自由度为n的卡方分布时，随机变量t：

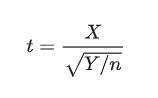
服从一个自由度为n的t分布。阅读上述定义似乎与我们要做的事情毫无关联，但且让我们来找出两个符合上述要求的随机变量出来后，再来品味一番。

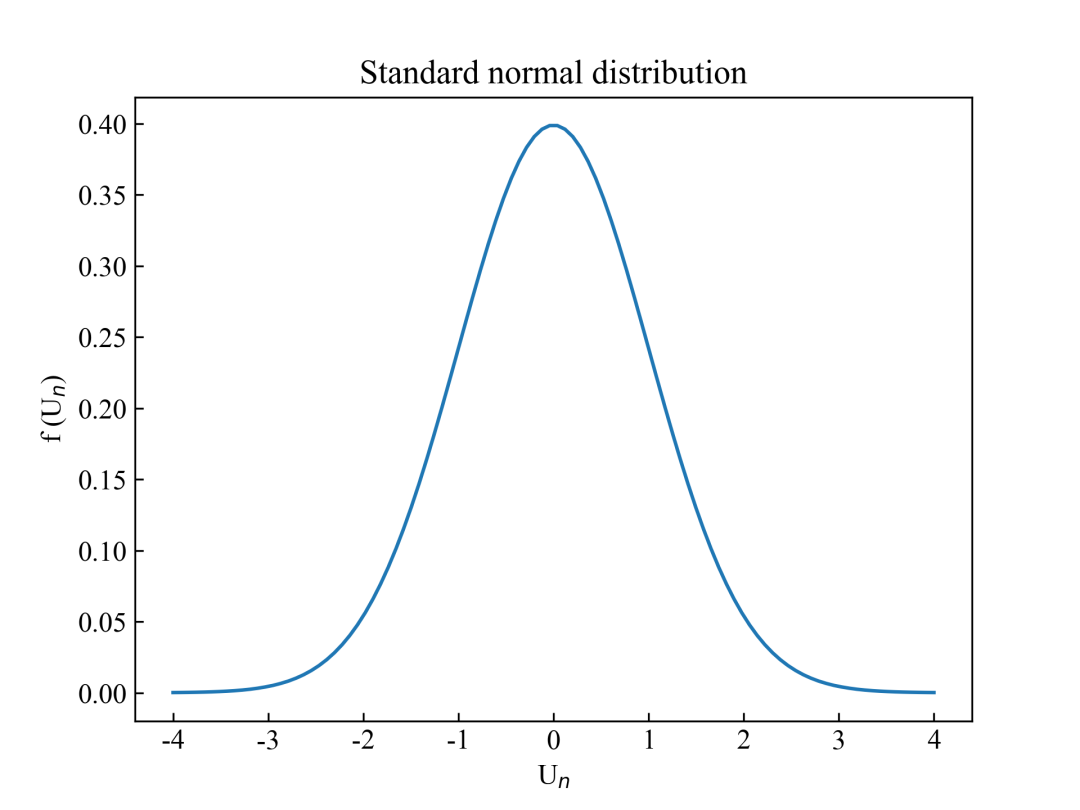
服从标准正态分布的随机变量X：概率论中有一个很强大的定理叫做中心极限定理：假设n个独立且完全相同的随机变量X1，X2，X3……Xn，期望均为μ  ，总体方差均为σ²。则存在一个随机变量Un：

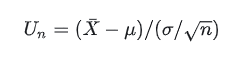
当n趋向于无穷大时， Un 服从标准正态分布。

服从自由度为n-1卡方分布的随机变量Y：设X1, X2, ... Xn是来自服从正态分布总体的随机变量，则样本方差与总体方差之比服从一个自由度为n-1的卡方分布：

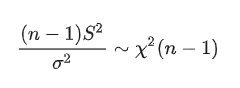
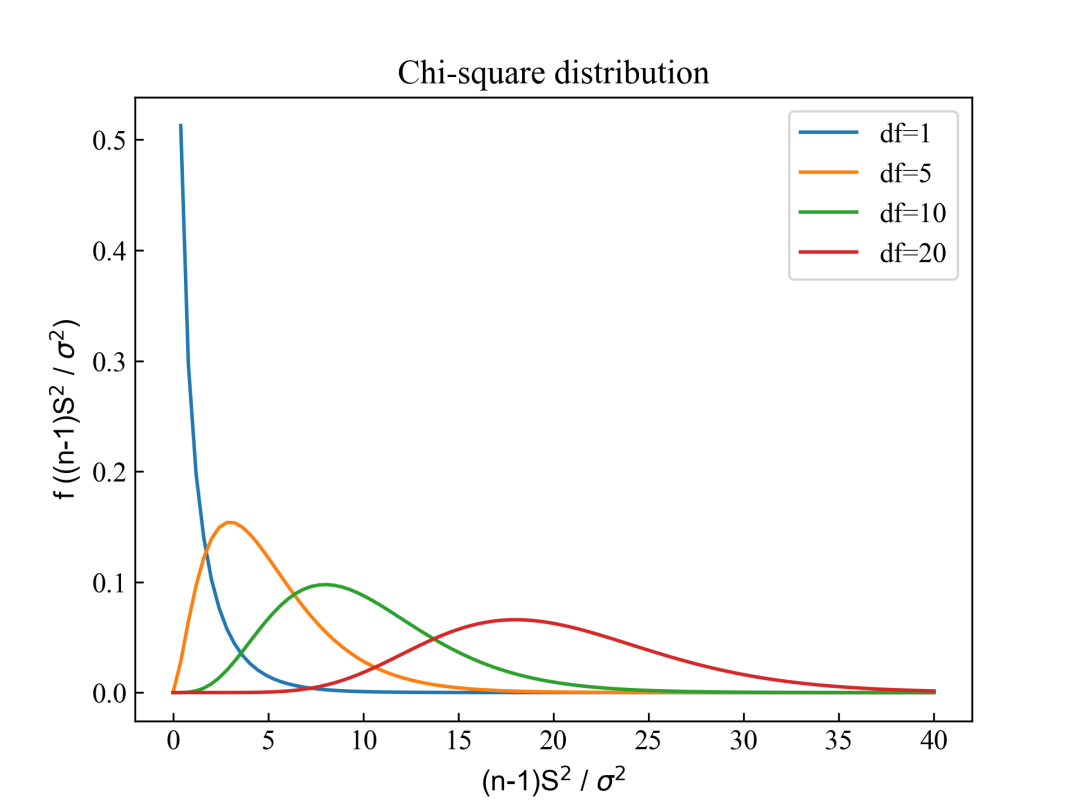
接下来我们将上述两个随机变量

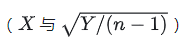
相除：

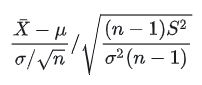
化简后得到下述公式：

通俗一些解释：当小明同学进行了一轮问卷试验时，相当于他在一个总体中（全国手机用户）进行了一次抽样调查，假如小明同学继续任劳任怨的进行第二轮、第三轮、第四轮....第m轮的问卷调查，当m趋向于无穷大，且在总体方差已知的情况下，m轮调查下来的问卷平均得分（这里我们先不管是苹果手机还是华为手机），将服从一个正态分布。但若将总体方差未知，用样本方差替换，将服从一个自由度为每次调查样本量-1的t分布。

2 假设检验与t检验

现在暂且让我们将小明同学的问题做一些变化。我们先不讨论苹果和华为之间孰强孰弱，假设有某一个权威机构发布过一份调查数据，说目前全国人民对自己手中智能手机的打分平均分为8分，我们想探究一下苹果和华为的用户是否达到了这一平均分？我们就利用刚刚所描述的理论解决这个问题。

首先我们知道，小明同学一共调查了120位智能手机用户，并没有将全国的用户都叫过来打分，因此总体均值和总体方差都是未知的。如果我们假设本次调查中用户对手机打分的总体均值与权威机构发布的全国调研报告一致（ H0 假设），那么此次抽样调查的t值： 

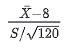
就应该属于一个自由度为119的t分布。

我们知道，所有的分布都会对应一个概率密度函数，通过计算得到的t值，我们可以查表找到它落在自由度为119的t分布上的概率（p值），如果这个概率小于0.05（个别领域会选用p值取值为0.1），则认为假设发生是一个不可能事件，从而拒绝原假设，反之则认为假设成立。

这种提出一个假设来“证伪”的方法，被叫做“假设检验”，而此次检验过程中用到了t分布来进行概率检验，所以被称为“t检验”。

前面已经介绍过，t分布所包含的卡方分布必须是基于正态分布总体才能成立的，所以我们每次做t检验之前都要先检验数据是否服从正态分布。

3 配对样本t检验

上述的检验方法中，我们考察的是一次抽样调查的结果与某一总体均值之间的比较，这种检验通常被称作单样本t检验。

但有些时候，我们总希望对一件事件发生的前后进行对比，观察受试群体有没有事件影响，例如调查一群新冠病人在吃特效药前后的体温变化，来判断特效药对新冠病人是否有降温作用；一群游戏玩家在领到丰厚奖励前后活跃度的对比，判断奖励是否提升了玩家游戏兴趣等。这些场景下，虽然调查被分了先后，会最终获得两份数据，但受试的对象都是同一批人，所以我们只需将前后两次的调查结果对应相减，判断相减后数据与总体均值0之间的关系即可，判断方法与单样本t检验完全一致，这就是配对样本t检验。

4 独立样本t检验

总算可以回归到华为和苹果手机谁的口碑更好这一问题上来了，既然有了配对样本t检验的前车之鉴，我们自然也希望能够将这两份数据相减，观察它们与0之间的关联程度。但这一次我们遇到了一个很强的阻力：受试群体不是同一批人。没关系，这难不倒我们，因为概率论中有这样一条定理：

由于关于独立样本t检验多出来的定理要求两样本总体方差要相等，因此在进行独立样本t检验时，要比前两种检验多出一个步骤：方差齐次性检验。

附录

附录是关于独立样本t检验的R语言代码：

其中"RData.csv"的数据如下所示，所示数据是A类土壤和B类土壤中速效氮含量的测定数据：

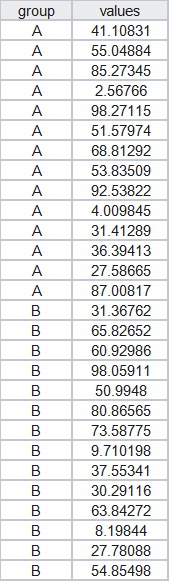
5 DMSAS独立样本t检验

上述对t分布和t检验做了详细解析，也融合了生动的案例学习，相信大家对t检验的检验步骤有了清晰的了解，感兴趣的朋友可以用上面附录中关于独立样本t检验的R语言代码来尝试做一下分析，但我们日常分析需求中也不用这么复杂，下面我给大家用我们第一款国产化科研级数据分析软件"DMSAS"来做一下独立样本t检验分析，数据案例就用上述"RData.csv"的数据来演示：

1. 先将这份数据导入到“DMSAS”中

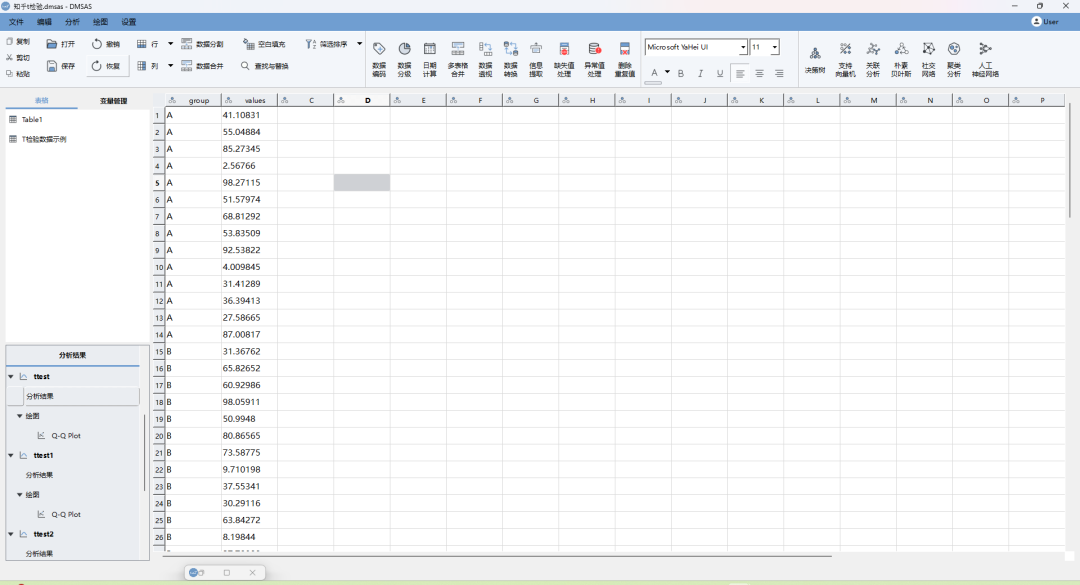
2. 点击“分析”，点击“t检验”，选择独立样本，将“values”放到待检验的变量中，将“group”放入到分组变量中

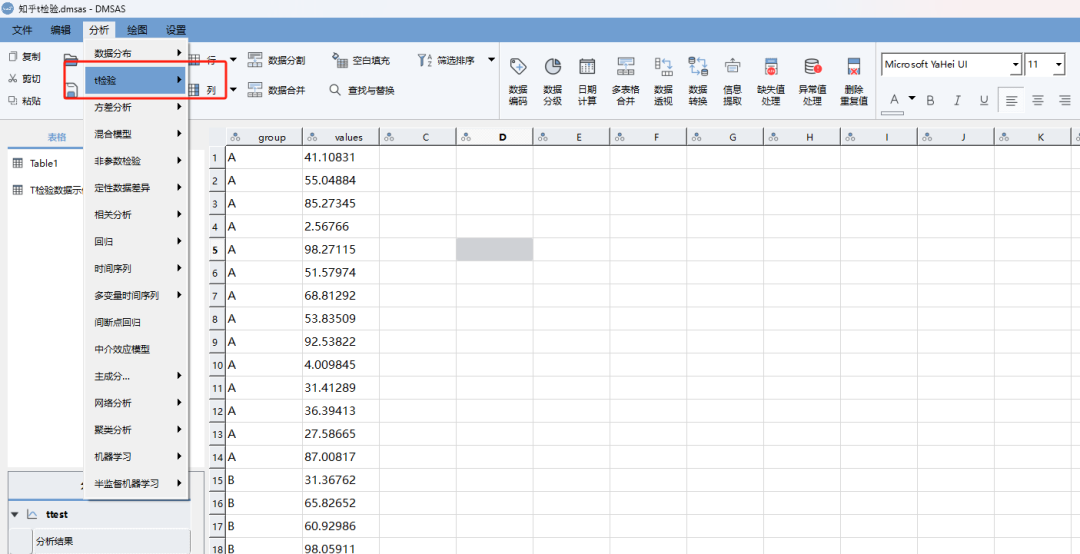
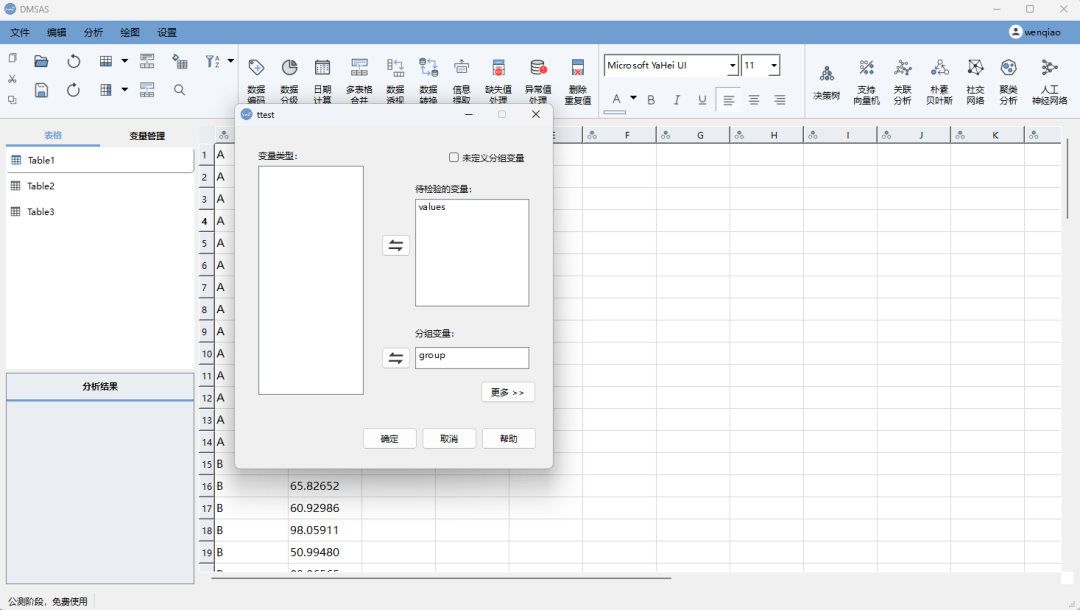
我们可以看到这款软件的操作界面简单清晰明了，哪怕是第一次使用的新手也能轻松上手。

3. 下面软件直接输出分析结果，包含了t检验的所有步骤和结果说明

（1）这是得出的描述性统计和均值置信区间

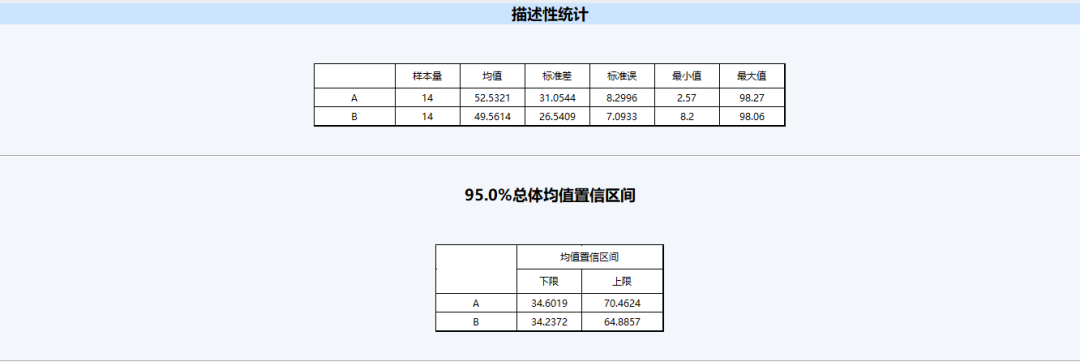
单从A和B两组的均值来看，我们能否得出A类土壤中速效氮含量高于B类土壤呢？我们再看看后面得出的t检验结果。

（2）这是得出的正态性检验和方差齐性检验

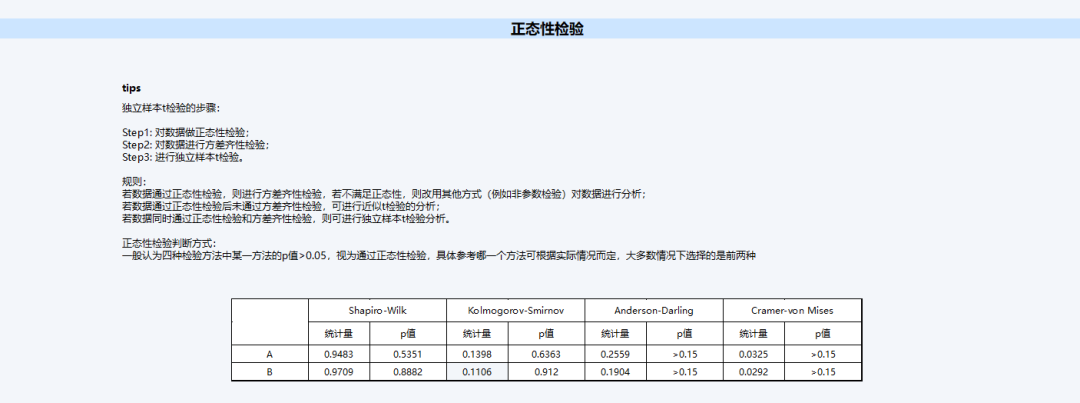
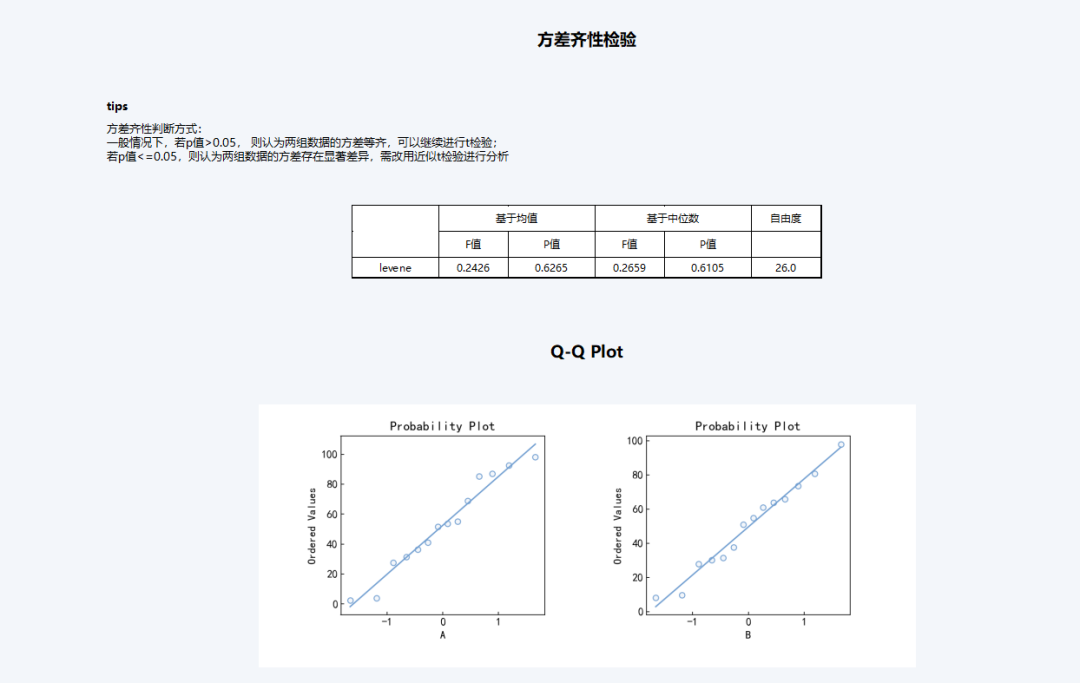
从结果上我们可以看到除了输出分析结果，软件还给出了独立样本t检验的步骤及规则、正态性检验判断方式和方差齐性判断方式，这对于初学者和新手非常友好，可以一站式解决我们的统计分析需求。

（3）这是得出的t检验结果

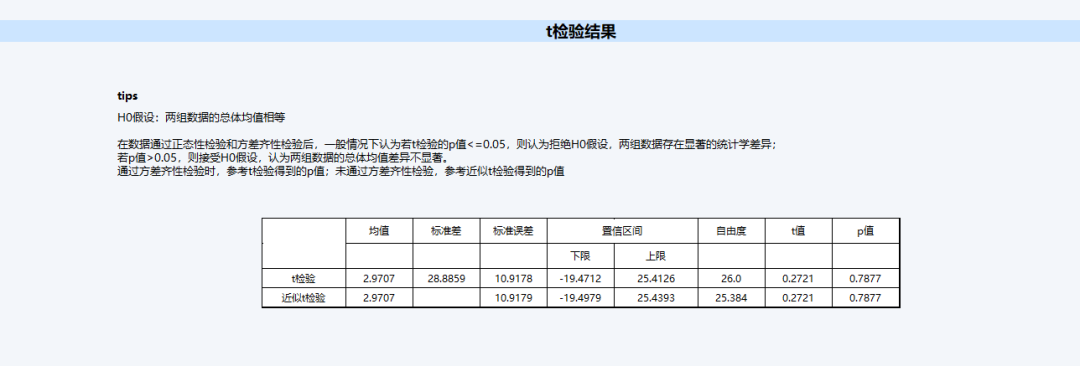
从t检验结果来看，p值均大于0.05，可以认为A和B两组数据的总体均值差异不显著。

以上就是本期文章对t分布和t检验的详细解析，从引入案例到理论知识，全局梳理了t分布和t检验的相关知识，还借助了我们第一款国产化科研级数据分析软件--DMSAS，对独立样本t检验的分析步骤做了一个清晰的演示，希望对正在学习的朋友们有所帮助！