方差分析 (ANOVA)和多重比较

logo
DMSAS

2025-10-10 18:30:04

方差分析 (ANOVA)和多重比较

太长不看版

方差分析（ANOVA）用于检验两个以上分组之间的差异；换句话说，如果要检验多组（两个以上）样本之间的差异，应选择方差分析。例如，检验某个指标的值是否随时间变化（时间点大于两个）时，就应使用方差分析。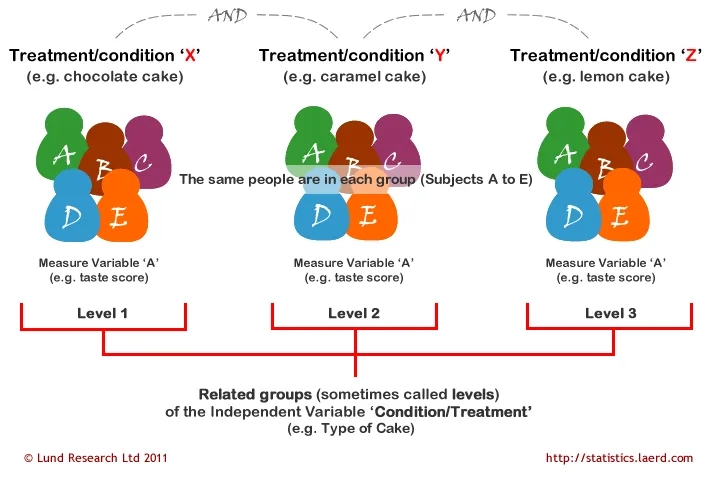方差分析通过比较不同组间的均值和组内方差来进行检验。它的核心思想是分析组间方差（各组均值之间的差异）与组内方差（各组内部数据的变异性）的比例关系，以确定组间差异是否显著。

a.一般而言，如果各组之间的均值差异较大，同时组内方差较小，则表明组间差异较大。这种情况下，自变量在因变量之间具有显著差异，因此应拒绝原假设（认为组间无显著差异）。

b.相反，如果各组之间的均值差异较小，同时数据的组内方差较大，则表明组间差异较小。这种情况下，自变量在因变量之间没有显著差异，因此应接受原假设（认为组间无显著差异）。

t检验无法替代方差分析，因为t检验仅用于比较两组之间的均值差异。如果对多个组使用多次t检验来代替方差分析，会增加第一类错误的概率（即假阳性），这被称为“多重比较问题”，而方差分析可通过Tukey HSD 检验、Bonferroni 校正等方法解决该问题。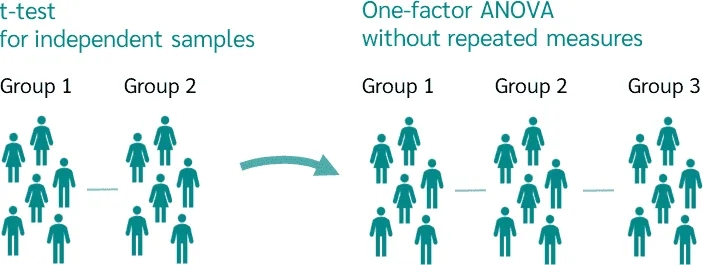分类

方差分析

根据分析因素的数量和实验设计的类型进行分类：

单因素方差分析（One-Way ANOVA）：用于比较一个因素下多个水平之间的差异，例如比较不同教学方法对学生成绩的影响。

双因素方差分析（Two-Way ANOVA）：用于比较两个因素的交互作用和各因素对结果变量的独立影响，例如研究不同肥料类型和浇水频率对植物生长的共同影响。

根据是否进行重复测量，还可以进一步分类为：

重复测量单因素方差分析（Repeated Measures One-Way ANOVA）：用于同一组受试者在不同时间点或条件下的多次测量，以分析时间或条件对结果变量的影响。

重复测量双因素方差分析（Repeated Measures Two-Way ANOVA）：用于多个因素（例如时间和处理条件）对同一组受试者的多次测量，以分析因素间的交互作用和独立效应。

多重比较

根据方差齐性和不齐性分为两类：

方差齐性相等的情况：LSD (Least Significant Difference)、Bonferroni、SNK (Student-Newman-Keuls)、Sidak、Duncan、Scheffe、Tukey HSD (Honestly Significant Difference)、Dunnett。

方差不齐的情况：Tamhane's T2、Dunnett's T3、Games-Howell。


啰唆版

什么是方差分析？

方差分析 (ANOVA) 用于检验是否在两个以上的样本之间存在统计显著性差异。为此，将各组的均值和方差相互比较。与 t 检验不同，t 检验用于检验两个样本之间是否存在差异，而 ANOVA 用于检验两个以上的组之间是否存在差异。

方差分析有不同的类型，其中最常见的是单因素和双因素方差分析。方差分析可分为有重复测量和无重复测量两种。根据样本是否独立或依赖，分别使用无重复测量或有重复测量的方差分析。如果同一人在多个时间点进行了访谈，样本是依赖样本，此时应使用有重复测量的方差分析。方差分析类别：

  1. 单因素（或单向）方差分析
  2. 双因素（或双向）方差分析
  3. 带重复测量的单因素 ANOVA
  4. 带重复测量的双因素 ANOVA

（此外还有多元方差分析，会单独撰写文章介绍）

方差分析（ANOVA） 的工作原理

方差分析（ANOVA）的工作原理是通过分析多个组内的方差水平，来判断这些组之间是否存在显著差异。具体来说，ANOVA 从每个组中抽取样本来进行比较。在 ANOVA 测试中，首先需要检查由自变量定义的每个组内的方差——这个方差是通过各个组中因变量的数值计算得到的。然后，将每个组内的方差与所有组均值的整体方差进行比较。


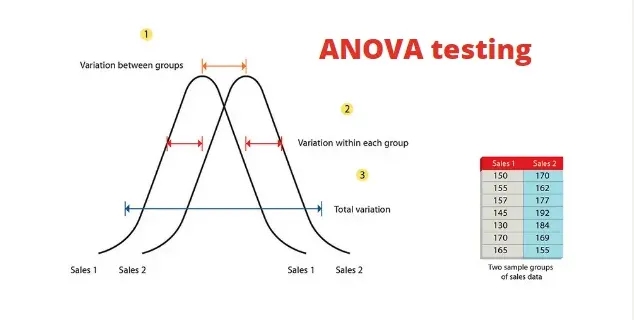
  1. 一般而言，如果各组之间的均值差异较大，同时组内方差较小，则表明组间差异较大。这种情况下，自变量在因变量之间具有显著差异，因此应拒绝原假设（认为组间无显著差异）。
  2. 相反，如果各组之间的均值差异较小，同时数据的组内方差较大，则表明组间差异较小。这种情况下，自变量在因变量之间没有显著差异，因此应接受原假设（认为组间无显著差异）。

可不可以计算多个 t 检验代替方差分析 （多重比较问题）？

这个问题其实回答的是为什么要用ANOVA。

当年课题组内有一位师兄投稿，初审的时候被reviewer argue，问为啥对多个因素（组别）的差异统计用多个t检验进行分析，而不是使用方差分析，并质疑由此得出的结论。所以搞好统计分析，对科研是很有帮助的，甚至是必须的。在这里聊一聊能不能计算多个 t 检验来代替方差分析。

虽然理论上来说，可以使用多个 t 检验来替代方差分析（ANOVA），但这种方法并不推荐，主要有以下几个原因：

  1. 增加第一类错误率和多重比较问题：每次进行 t 检验时，都会有一个预设的显著性水平（通常为 5% 或 p < 0.05），这表示我们接受错误结论的概率为 5%。如果对多个组进行多次 t 检验，这些个别的错误概率会累积，导致总体第一类错误率显著上升。这种累积错误称为“多重比较问题”。例如，如果对 5 个组进行配对比较（总共 10 次 t 检验），假设每次 t 检验的显著性水平为 0.05，那么实际的总错误概率将远超过 5%。这意味着，随着比较次数的增加，出现假阳性（错误拒绝原假设）的风险显著增加，导致研究结果不可靠。
  2. 效率低下和复杂性增加：当你比较 三个或更多组时，需要对每两个组进行一次 t 检验。随着组数的增加，所需的 t 检验次数会迅速增长。例如，4 组数据需要进行 6 次 t 检验，5 组需要 10 次，依此类推。这不仅增加了计算量和分析时间，还显著提高了累积的第一类错误风险。这种增加的复杂性和错误风险是多重比较问题的直接体现。
  3. 丢失整体信息和无法检验总体显著性：多个 t 检验只能分别比较每两个组之间的差异，无法给出所有组间差异的整体统计结论，并可能忽略一些更复杂的模式和交互效应。相反，方差分析（ANOVA）能够同时考虑所有组之间的差异，提供一个关于组间总变异的综合分析，并一次性检测多组之间的总体差异。在 ANOVA 中，如果结果显示有显著的总体差异，研究者还可以进一步进行事后多重比较检验（如 Tukey HSD、Bonferroni 校正等），以确定哪些具体组之间存在差异，并在控制总体错误率的前提下得出可靠的结论。
  4. 多重比较控制和效能保障：ANOVA 之后的多重比较方法（如 Tukey HSD 检验、Bonferroni 校正等）专门设计用来解决多重比较问题。这些方法能够有效地控制整体的第一类错误率，同时进行多组间的配对比较。而简单地使用多个 t 检验，无法实现对整体错误率的有效控制。因此，在需要比较多组数据时，使用 ANOVA 结合事后多重比较方法可以提供更高的效能和准确性。

因此，当需要比较三个或更多组时，使用 ANOVA 是更优的方法。虽然在统计分析中计算多个 t 检验来比较多组数据是可能的，但这种方法会引发多重比较问题，显著增加整体错误概率，从而降低分析的可靠性。相反，使用方差分析（ANOVA）不仅可以一次性检测多组之间的总体差异，还可以通过适当的多重比较校正方法进一步分析具体的组间差异，在保证分析准确性的同时控制整体错误率。

在科研实践中，选择 ANOVA 是更为合理和科学的方法。例如，每个假设检验都有一定的错误概率。通常将错误概率设定为 5%，从纯统计角度来看，每 20 个检验中就有一个会得出错误结果。例如，如果比较 20 个实际上没有差异的组，其中一个检验可能会由于抽样原因显示出显著差异。

多重比较的方法


从上面的表述中，大家应该意识到多重比较是方差分析中非常关键的一步，所以需要单独介绍一下。方差分析（ANOVA）后用于多重比较有多种方法，这些方法根据方差齐性和不齐性分为两类：

1.方差齐性相等的情况

  1. LSD(LeastSignificant Difference)：适用于方差齐且样本量相等的情况，计算组间均值差异的最小显著性差异。该方法敏感但不太保守，容易出现第一类错误。
  2. Bonferroni：用于控制多重比较中的错误率，通过调整显著性水平来限制总体第一类错误概率。较为保守，适用于任意方差齐性和样本量。
  3. SNK(Student-Newman-Keuls)：用于多重比较，排序组均值并比较相邻组之间的差异，适用于方差齐性相等的情况。
  4. Sidak：类似于 Bonferroni 校正，但校正方式更为精细，特别在处理大量比较时更有效。
  5. Duncan：用于多重比较分析，类似 SNK，但更宽松，允许更多的差异被认为显著。
  6. Scheffe：非常保守的多重比较方法，适用于样本量不等和方差齐性假设。允许用户测试所有可能的线性组合。
  7. TukeyHSD(Honestly Significant Difference)：用于所有成对组比较，适用于方差齐性相等的情况，能够很好地控制整体的错误率。
  8. Dunnett：用于将多个实验组与单个对照组进行比较，适合方差齐性相等的情况。

2.方差不齐的情况

  1. Tamhane's T2：适用于方差不齐且样本量不等的情况，是一种保守的事后检验方法
  2. Dunnett's T3：用于方差不齐时，尤其适合样本量不等的情况。
  3. Games-Howell：在方差不齐和样本量不等的情况下非常有效，是处理这些情况的最佳方法之一。

这些多重比较方法根据数据特征和假设前提的不同，适合用于不同的统计检验情境，从而帮助我们在控制错误率的前提下，确定具体组间的显著差异。上述方法在DMSAS中都可以非常便捷的实现。

方差分析结果解读

对于方差分析的数学计算过程，网上资料已经很是详尽了，这里就不赘述这一部分。感兴趣的可以去学习下，我现在是不感兴趣了，所以就不多写了，因为我是每次看完就忘，而且平时也不会真的自己套公式去手动计算，都是软件自动计算，比如DMSAS就可以非常方便得进行ANOVA分析。这就是我偷懒的理由，连粘贴都懒得贴了，给大家一个图看看就可以了。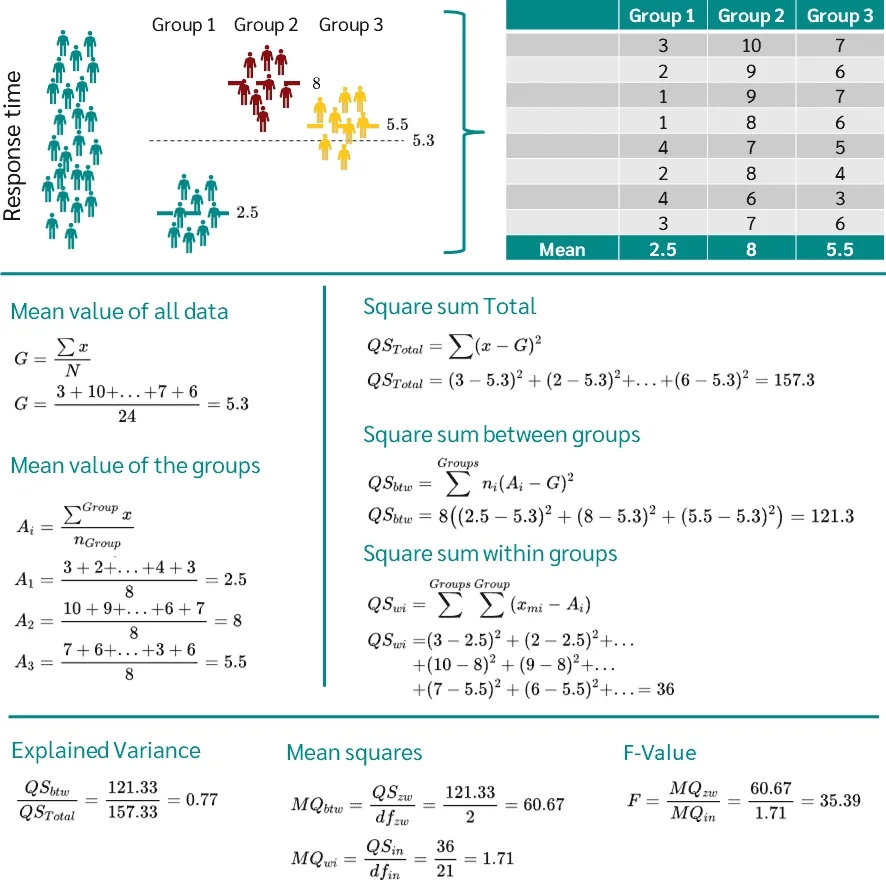但是对方差结果的解读是必须要了解，如果连结果都看不懂做这个分析就没意义了。

1.解释输出结果

在 ANOVA 中，F 值、自由度（df） 和 p 值 共同构成假设检验的核心，它们共同提供了数据的完整图景，使我们能够对研究问题做出决策。

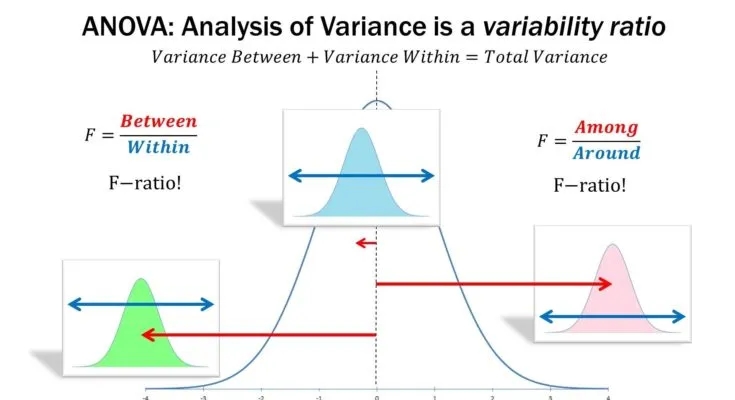F 值和自由度共同用于计算 p 值：p 值用于判断组间差异是否是由于偶然因素造成的。通常，如果 p 值小于 0.05，我们认为结果具有统计学显著性，即这些差异不太可能是由于随机因素导致的。

  1. F 值：衡量组间变异性与组内变异性的比率，这是 ANOVA 中的基本统计量，用来量化组均值之间的相对差异程度。
  2. 自由度（df）：需要根据组数和观测数量调整 F 值，考虑到样本量和组数对分析结果的可靠性和准确性的影响。
  3. p 值：将 F 值及其自由度转化为一种概率，帮助你对原假设做出决策。p 值提供了分析的统计学显著性，并使结果更直观易懂。

2.事后检验（Post-hoc testing）

如果使用 ANOVA 发现了显著的效果，意味着至少有两个组之间存在显著差异，但它并不能具体指出哪些组之间的差异显著。为此，需要进行事后检验（Post-hoc tests），也就是上述提到得多重比较。事后检验就是为了进行多重比较以确定哪些组之间存在显著差异。使用 ANOVA 检测到显著差异后，事后检验方法帮助研究者进一步探讨数据中的具体差异，同时控制统计分析中的错误风险。

DMSAS中方差分析实战

1.研究目的和示例数据

  1. 研究目的：研究不同肥料和光照条件对植物生长的影响
  2. 研究背景：假设我们想研究两种不同的肥料类型（有机肥料A和化学肥料B）以及三种不同的光照条件（低光照、中等光照和高光照）对一种特定植物（如小麦）生长的影响。研究的主要目标是确定肥料类型和光照条件对植物生长的综合效果，以及它们之间是否存在交互作用。
  3. 变量：

   1.自变量（因素）：

   肥料类型：有机肥料A、化学肥料B

（2个水平）

   光照条件：低光照、中等光照、高光照（3个水平）

   2.因变量：植物生长高度（厘米）

数据情况如下：

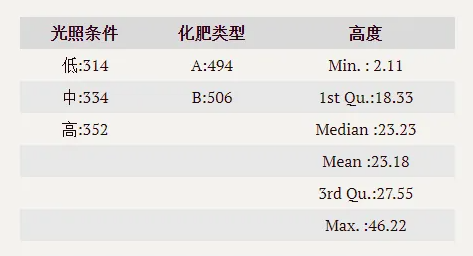
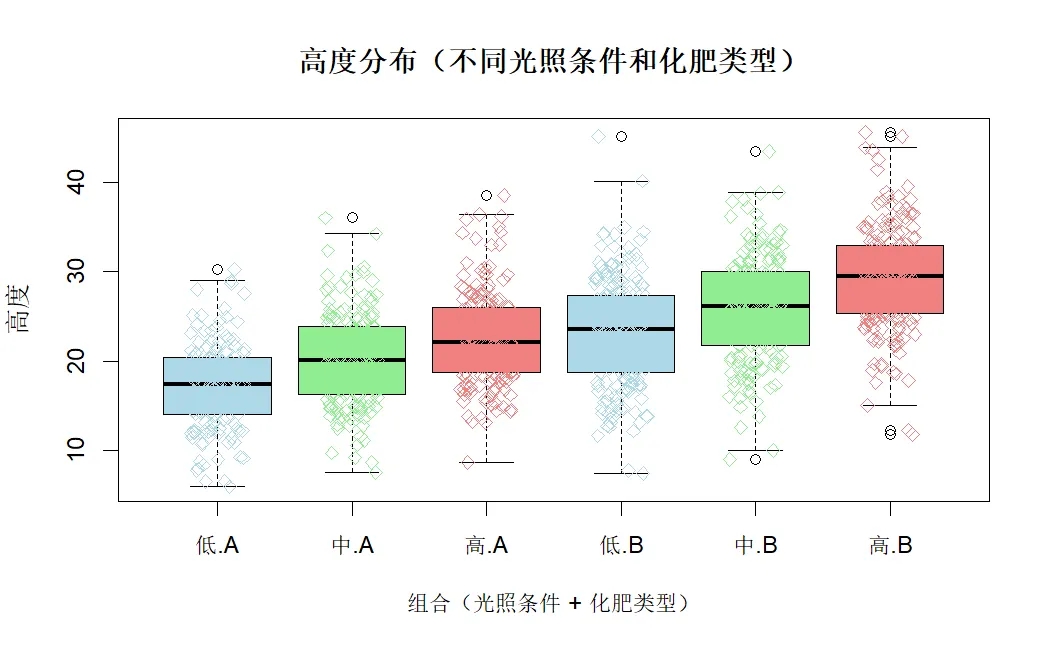2.DMSAS操作

  1. 导入数据：将数据导入表格，确保数据格式正确。
  2. 从菜单栏分析按钮中选择-分析-方差分析-多因素
  3. 选择待分析的变量：选择 “高度” 。
  4. 因子变量：选择 “光照条件”和“化肥类型” 。

点击“更多”设置：

   a.为考察“光照条件”和“化肥类型”的交互作用是否显著，我们先在构建项菜单中构建出二者交互作用的变量纳入分析。

b.多重比较因子：选择 “光照条件”和“化肥类型” 。

c.多重比较方法：有多种多重比较方法供大家选择， 本次分析我们选用TukeyHSD。

 d.lsmeans：本次研究中还需考察“光照条件”与“化肥类型”的交互作用，因此免不了要考察当固定某个因素在一个水平时，另外一个因素各水平均值之间是否存在显著差异，因此我们在lsmeans中将交互因素选入右侧“待分析变量”，勾选“多重比较”选择框。

点击“确定”：运行ANOVA分析，查看结果。

DMSAS有非常详尽的结果输出。

3.结果解读

首先DMSAS的结果中，对数据的概况进行统计描述，并输出方差分析的结果。

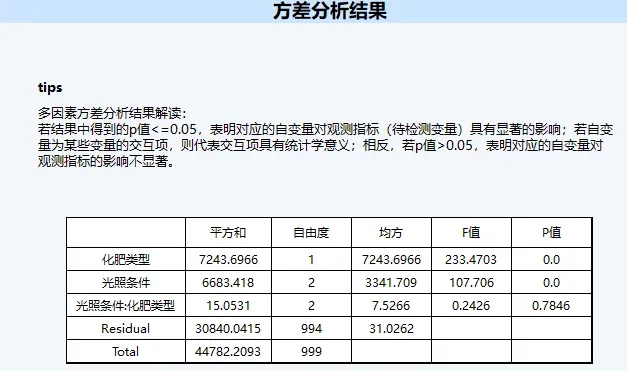从方差表中可以看到，关于化肥类型和光照条件计算的均方和F值，以及最关键的p值。结果显示，该数据的p值远小于0，表明差异极为显著。然而两者的交互作用检验得到的p值=0.7846（p值>0.05）表明二者不存在交互作用。因此无需解读lsmeans计算得到的分析结果。

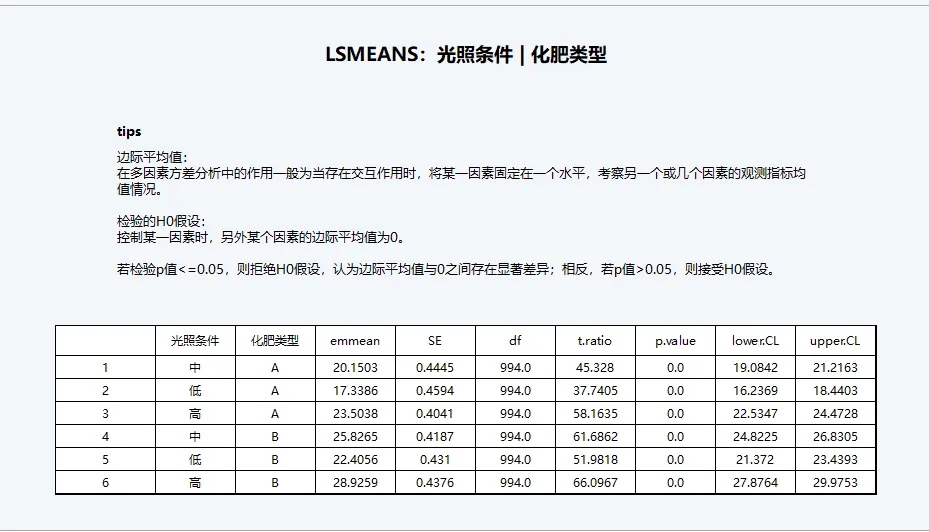
根据分析结果，不同的“化肥类型”会显著影响植物生长高度，而化肥类型只有A和B两种，因此不难推断出两种化肥类型的作用效果对植物的生长的影响具有显著差异。而“光照条件”却含有三个分类，因此具体是哪两种分类具有显著影响，而哪两种不显著，则要进一步查阅多种比较的分析结果。

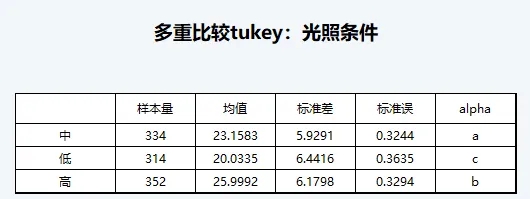
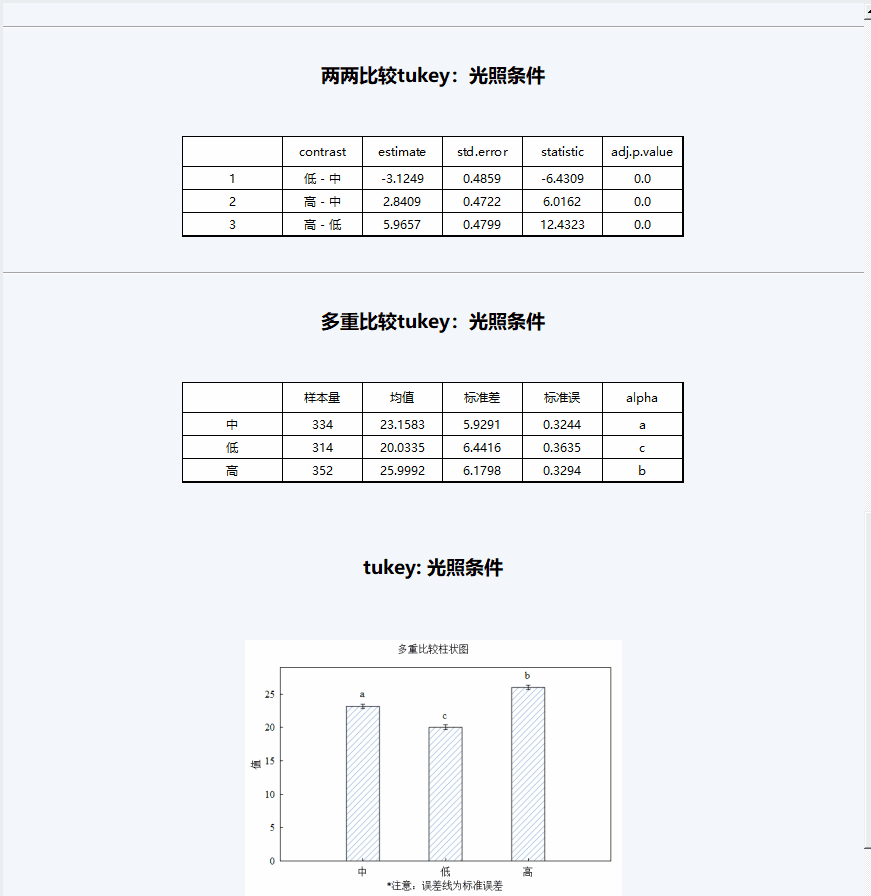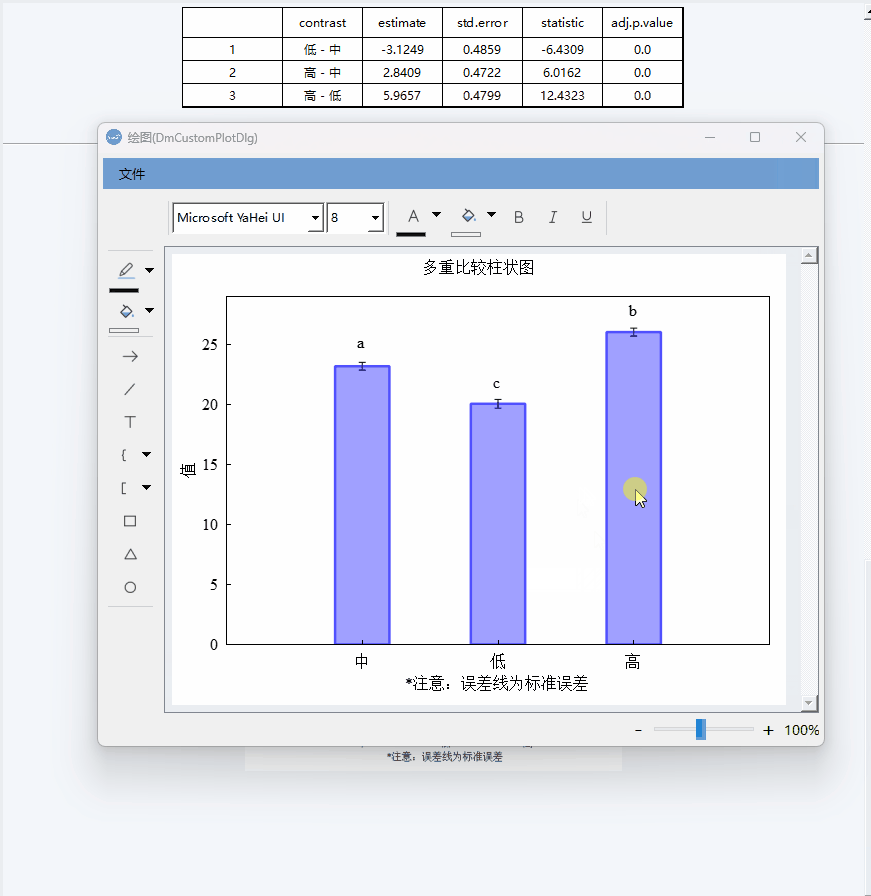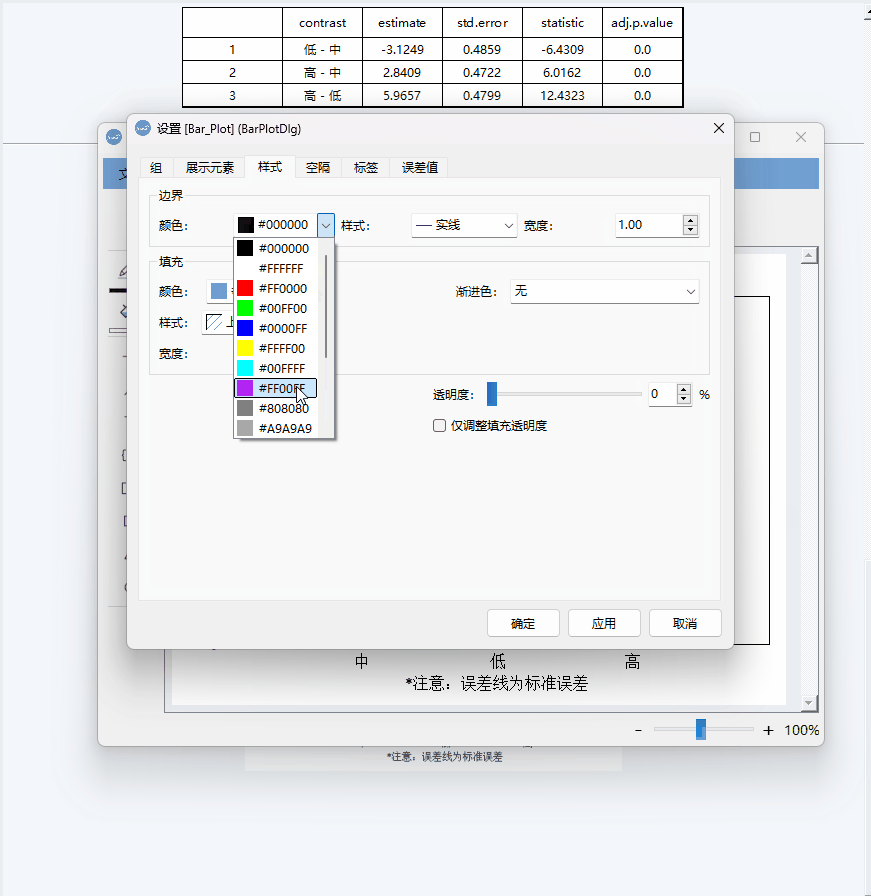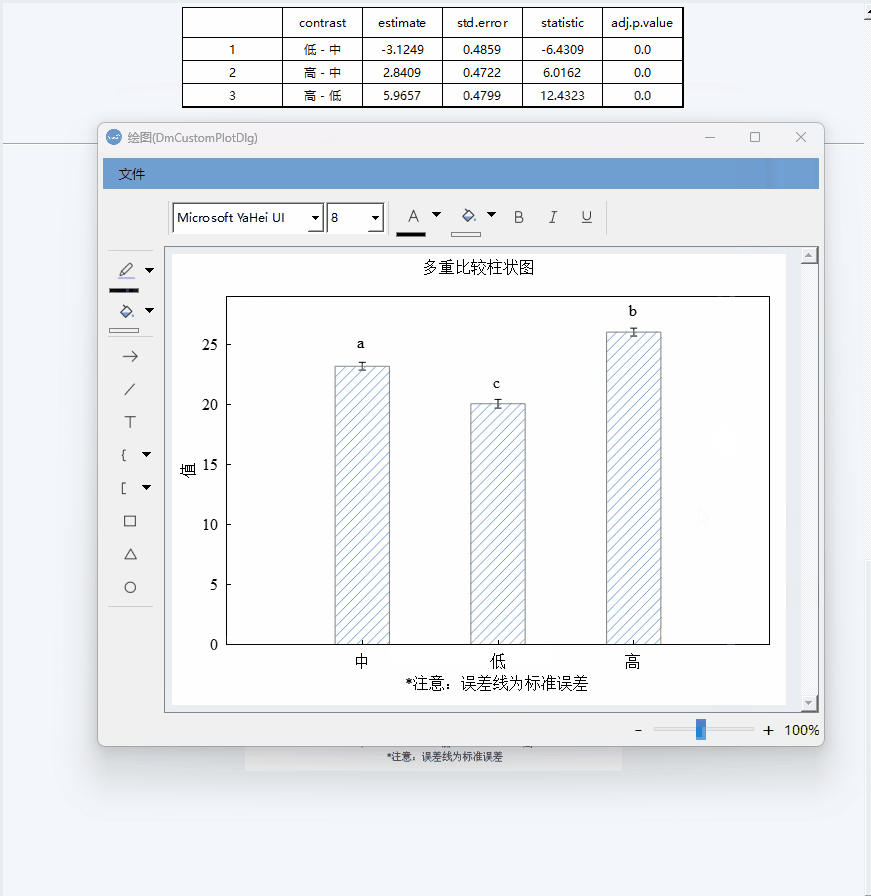
从DMSAS中输出的多重比较结果来看，光照条件的各组因素均存在显著差异。

DMSAS中对于多重比较的差异显著用字母标注法。

DMSAS中进行ANOVA分析，对于绝大非统计专业的使用者来讲是非常便捷的，而且输出的结果清晰明了，极大了节省了数据分析的时间，可以让大家专注于所研究的问题本身。